Estimating Conventional lndex Pages

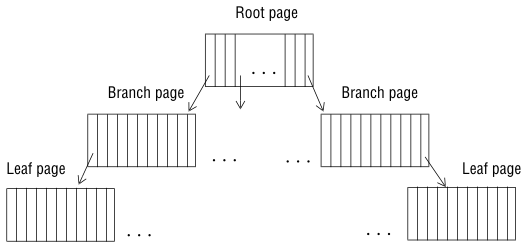
As Figure 34 shows, an index is arranged as a hierarchy of pages (technically, a B-tree). The topmost level of the hierarchy contains a single root page. Intermediate levels, when needed, contain branch pages. Each branch page contains entries that see a subset of pages in the next level of the index. The bottom level of the index contains a set of leaf pages. Each leaf page contains a list of index entries that see rows in the table.

The number of levels needed to hold an index depends on the number of unique keys in the index and the number of index entries that each page can hold. The number of entries per page depends, in turn, on the size of the columns being indexed.

If the index page for a given table can hold 100 keys, a table of up to 100 rows requires a single index level: the root page. When this table grows beyond 100 rows, to a size between 101 and 10,000 rows, it requires a two-level index: a root page and between 2 and 100 leaf pages. When the table grows beyond 10,000 rows, to a size between 10,001 and 1,000,000 rows, it requires a three-level index: the root page, a set of 100 branch pages, and a set of up to 10,000 leaf pages.

Index entries contained within leaf pages are sorted in key-value order. An index entry consists of a key and one or more row pointers. The key is a copy of the indexed columns from one row of data. A row pointer provides an address used to locate a row that contains the key. A unique index contains one index entry for every row in the table.

To estimate the number of index pages

Add up the total widths of the indexed column or columns.
This value is referred to as colsize. Add 4 to colsize to obtain keysize, the actual size of a key in the index.

For example, if colsize is 6, the value of keysize is 10.
Calculate the expected proportion of unique entries to the total number of rows.
The formulas in subsequent steps see this value as propunique.

If the index is unique or has few duplicate values, use 1 for propunique.

If a significant proportion of entries are duplicates, divide the number of unique index entries by the number of rows in the table to obtain a fractional value for propunique. For example, if the number of rows in the table is 4,000,000 and the number of unique index entries is 1,000,000, the value of propunique is .25.

If the resulting value for propunique is less than .01, use .01 in the calculations that follow.
Estimate the size of a typical index entry with one of the following formulas, depending on whether the table is fragmented or not:
1. For nonfragmented tables, use the following formula:
```
entrysize = (keysize * propunique) + 5 + 4
```
  The value 5 represents the number of bytes for the row pointer in a nonfragmented table.
  
  For nonunique indexes, the database server stores the row pointer for each row in the index node but stores the key value only once. The entrysize value represents the average length of each index entry, even though some entries consist of only the row pointer. For example, if propunique is .25, the average number of rows for each unique key value is 4. If keysize is 10, the value of entrysize is 7.5. The following calculation shows the space required for all four rows:
```
space for four rows = 4 * 7.5 = 30
```
  This space requirement is the same when you calculate it for the key value and add the four row pointers, as the following formula shows:
```
space for four rows = 10 + (4 * 5) = 30
```
2. For fragmented tables, use the following formula:
```
entrysize = (keysize * propunique) + 9 + 4
```
  The value 9 represents the number of bytes for the row pointer in a fragmented table.
Estimate the number of entries per index page with the following formula:
```
pagents = trunc(pagefree/entrysize)
```
pagefree

is the page size minus the page header (2020 for a 2-kilobyte page size).

entrysize

is the value that you estimate in step 3.

The trunc() function notation indicates that you should round down to the nearest integer value.
Estimate the number of leaf pages with the following formula:
```
leaves = ceiling(rows/pagents) 
```
rows

is the number of rows that you expect to be in the table.

pagents

is the value that you estimate in step 4.

The ceiling() function notation indicates that you should round up to the nearest integer value.
Estimate the number of branch pages at the second level of the index with the following formula:
```
branches₀ = ceiling(leaves/node_ents)
```
Calculate the value for node_ents with the following formula:
```
node_ents = trunc( pagefree / ( keysize + 4) + 4)
```
pagefree

is the same value as in step 4.

keysize

is the colsize plus 4 obtained in step 1.

In the formula, 4 represents the number of bytes for the leaf node pointer.
If the value of branches₀ is greater than 1, more levels remain in the index.
To calculate the number of pages contained in the next level of the index, use the following formula:
```
branches_n+1 = ceiling(branches_n/node_ents)
```
branches_n

is the number of branches for the last index level that you calculated.

branches_n+1

is the number of branches in the next level.

node_ents

is the value that you estimated in step 6.
Repeat the calculation in step 7 for each level of the index until the value of branches_n+1equals 1.
Add up the total number of pages for all branch levels calculated in steps 6 through 8. This sum is called branchtotal.
Use the following formula to calculate the number of pages in the compact index:
```
compactpages = (leaves + branchtotal)
```
If your database server instance uses a fill factor for indexes, the size of the index increases.
The default fill factor value is 90 percent. You can change the fill factor value for all indexes with the FILLFACTOR configuration parameter. You can also change the fill factor for an individual index with the FILLFACTOR clause of the CREATE INDEX statement in SQL.

To incorporate the fill factor into your estimate for index pages, use the following formula:
```
indexpages = 100 * compactpages / FILLFACTOR
```

The preceding estimate is a guideline only. As rows are deleted and new ones are inserted, the number of index entries can vary within a page. This method for estimating index pages yields a conservative (high) estimate for most indexes. For a more precise value, build a large test index with real data and check its size with the oncheck utility.