Defining the Relationships

After you choose your database entities, you need to consider the relationships between them. Relationships are not always obvious, but all the ones worth recording must be found. The only way to ensure that all the relationships are found is to list all possible relationships exhaustively. Consider every pair of entities A and B and ask, "What is the relationship between an A and a B?"

A relationship is an association between two entities. Usually, a verb or preposition that connects two entities implies a relationship. A relationship between entities is described in terms of connectivity, existence dependency, and cardinality.

Connectivity

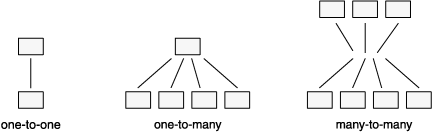
Connectivity refers to the number of entity instances. An entity instance is a particular occurrence of an entity. Figure 3 shows that the three types of connectivity are one-to-one (written 1:1), one-to-many (written 1:n), and many-to-many (written m:n).

Figure 3. Connectivity in Relationships

For instance, in the telephone directory example, an address can be associated with more than one name. The connectivity for the relationship between the address and name entities is one-to-many (1:n).

Existence Dependency

Existence dependency describes whether an entity in a relationship is optional or mandatory. Analyze your business rules to identify whether an entity must exist in a relationship. For example, your business rules might dictate that an address must be associated with a name. Such an association indicates a mandatory existence dependency for the relationship between the name and address entities. An example of an optional existence dependency could be a business rule that says a person might or might not have children.

Cardinality

Cardinality places a constraint on the number of times an entity can appear in a relationship. The cardinality of a 1:1 relationship is always one. But the cardinality of a 1:n relationship is open; n could be any number. If you need to place an upper limit on n, you specify a cardinality for the relationship. For instance, in a store sale example, you could limit the number of sale items that a customer can purchase at one time. You usually use your application program or stored procedure language (SPL) to place cardinality constraints.

Discovering the Relationships

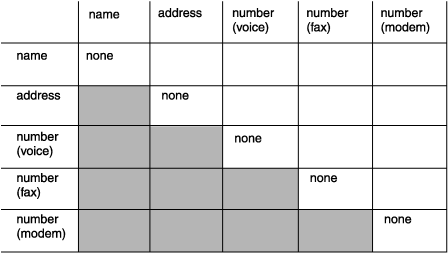
A convenient way to discover the relationships is to prepare a matrix that names all the entities on the rows and again on the columns. The matrix in Figure 4 reflects the entities for the personal telephone directory.

Figure 4. A Matrix That Reflects the Entities for a Personal Telephone Directory

You can ignore the shaded portion of the matrix. You must consider the diagonal cells; that is, you must ask the question, "What is the relationship between an A and another A?" In this model, the answer is always none. No relationship exists between a name and a name or an address and another address, at least none that you need to record in this model. When a relationship exists between an A and another A, you have found a recursive relationship. (See Resolving Other Special Relationships.)

For all cells for which the answer is clearly none, write none in the matrix. Figure 5 shows the current matrix.

Figure 5. A Matrix with Initial Relationships Included

Although no entities relate to themselves in this model, this situation is not always true in other models. A typical example is an employee who is the manager of another employee. Another example occurs in manufacturing, when a part entity is a component of another part.

In the remaining cells, write the connectivity relationship that exists between the entity on the row and the entity on the column. The following kinds of relationships are possible:

• One-to-one (1:1), in which not more than one entity A exists for one entity B and not more than one B for one A.
• One-to-many (1:n), in which more than one entity A never exists, but several entities B can be related to A (or vice versa).
• Many-to-many (m:n), in which several entities A can be related to one B and several entities B can be related to one A.

One-to-many relationships are the most common. The telephone directory model shows one-to-many and many-to-many relationships.

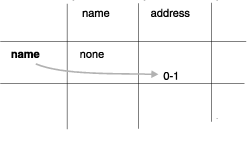
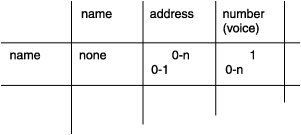
As Figure 5 shows, the first unfilled cell represents the relationship between names and addresses. What connectivity lies between these entities? You might ask yourself, "How many names can be associated with an address?" You decide that a name can have zero or one address but no more than one. You write 0-1 opposite name and below address, as Figure 6 shows.

Figure 6. Relationship Between Name and Address

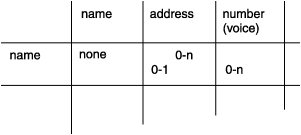
Ask yourself how many addresses can be associated with a name. You decide that an address can be associated with more than one name. For example, you can know several people at one company or more than two people who live at the same address.

Can an address be associated with zero names? That is, should it be possible for an address to exist when no names use it? You decide that yes, it can. Below address and opposite name, you write 0-n, as Figure 7 shows.

Figure 7. Relationship Between Address and Name

If you decide that an address cannot exist unless it is associated with at least one name, you write 1-n instead of 0-n.

When the cardinality of a relationship is limited on either side to 1, it is a 1:n relationship. In this case, the relationship between names and addresses is a 1:n relationship.

Now consider the next cell in Figure 5: the relationship between a name and a voice number. How many voice numbers can a name be associated with, one or more than one? When you look at your telephone directory, you see that you have often noted more than one telephone number for a person. A busy salesperson might have a home number, an office number, a paging number, and a car phone number. But you might also have names without associated numbers. You write 0-n opposite name and below number (voice), as Figure 8 shows.

Figure 8. Relationship Between Name and Number

What is the other side of this relationship? How many names can be associated with a voice number? You decide that only one name can be associated with a voice number. Can a number be associated with zero names? You decide you do not need to record a number unless someone uses it. You write 1 under number (voice) and opposite name, as Figure 9 shows.

Figure 9. Relationship Between Number and Name

To fill out the rest of the matrix in the same fashion, take the following factors into account:

• A name can be associated with more than one fax number; for example, a company can have several fax machines. Conversely, a fax number can be associated with more than one name; for example, several people can use the same fax number.
• A modem number must be associated with exactly one name. (This is an arbitrary decree to complicate the example; accept it as a requirement of the design.) However, a name can have more than one associated modem number; for example, a company computer can have several dial-up lines.
• Although some relationship exists between a voice number and an address, a modem number and an address, and a fax number and an address in the real world, none needs to be recorded in this model. An indirect relationship already exists through name.

Figure 10 shows a completed matrix.

Figure 10. A Completed Matrix for a Telephone Directory

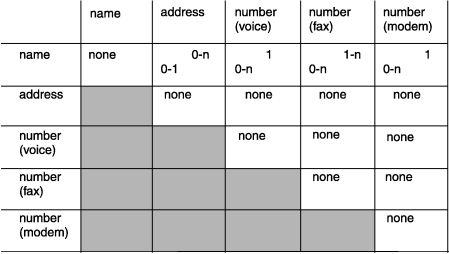
Other decisions that the matrix reveals are that no relationships exist between a fax number and a modem number, between a voice number and a fax number, or between a voice number and a modem number.

You might disagree with some of these decisions (for example, that a relationship between voice numbers and modem numbers is not supported). For the sake of this example, these are our business rules.

Diagramming Relationships

For now, save the matrix that you created in this section. You will learn how to create an E-R diagram in Diagramming Data Objects.